刷题时间:2021/03/28-2021/04/01
数据结构实验之二叉树
一:树的同构
Description
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。
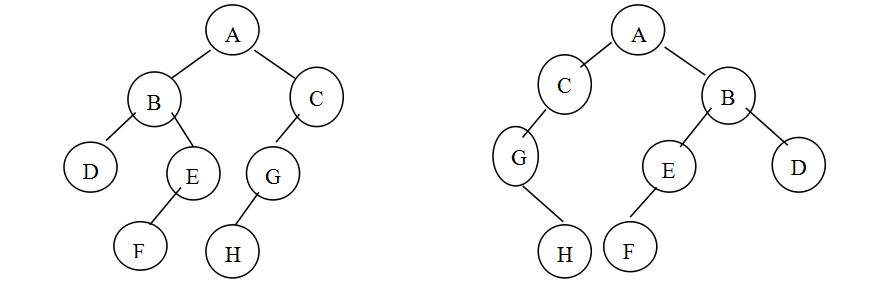
图1

图2
现给定两棵树,请你判断它们是否是同构的。
Input
输入数据包含多组,每组数据给出2棵二叉树的信息。对于每棵树,首先在一行中给出一个非负整数N (≤10),即该树的结点数(此时假设结点从0到N−1编号);随后N行,第i行对应编号第i个结点,给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空,则在相应位置上给出”-”。给出的数据间用一个空格分隔。
注意:题目保证每个结点中存储的字母是不同的。
Output
如果两棵树是同构的,输出“Yes”,否则输出“No”。
Sample
Input
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
Output
Yes
Hint
测试数据对应图1
参考代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int n1,n2;
struct node
{
char key;
int l,r;
}tree1[21],tree2[21];
void buildtree(struct node tree[],int n)
{
int i;
char s;
for(i=0;i<n;i++)
{
scanf("%s",&s);
tree[i].key=s;
scanf("%s",&s);
if(s=='-'){
tree[i].l=11;//把空值=11
}else{
tree[i].l=s-'0';
}
scanf("%s",&s);
if(s=='-'){
tree[i].r=11;
}else {
tree[i].r=s-'0';
}
}
}
//判断tree1和tree2子左右节点是不是互换就相等
int checkc(int i,int j)
{
if(tree1[tree1[i].l].key==tree2[tree2[j].l].key&&tree1[tree1[i].r].key==tree2[tree2[j].r].key)
return 1;
if(tree1[tree1[i].l].key==tree2[tree2[j].r].key&&tree1[tree1[i].r].key==tree2[tree2[j].l].key)
return 1;
return 0;
}
int check()
{
int i,j;
for(i=0;i<n1;i++)
{
for(j=0;j<n2;j++)//遍历,在tree2中去找与tree1相同的结点
{
if(tree1[i].key==tree2[j].key){
if(checkc(i,j))break;//这个判断完成了,则跳出,去判断下一个i
else return 0;
}
}
if(j==n2)return 0;
}
return 1;
}
int main()
{
while(~scanf("%d",&n1))
{
buildtree(tree1,n1);
scanf("%d",&n2);
buildtree(tree2,n2);
if(n1!=n2)printf("No\n");//n1!=n2那还判断个锤子。
else if(check())
printf("Yes\n");
else printf("No\n");
}
return 0;
}
二:遍历二叉树
Description
已知二叉树的一个按先序遍历输入的字符序列,如abc,,de,g,,f,,, (其中,表示空结点)。请建立二叉树并按中序和后序的方式遍历该二叉树。
Input
连续输入多组数据,每组数据输入一个长度小于50个字符的字符串。
Output
每组输入数据对应输出2行:
第1行输出中序遍历序列;
第2行输出后序遍历序列。
Sample
Input
abc,,de,g,,f,,,
Output
cbegdfa
cgefdba
Hint
参考代码
#include<stdio.h>
#include<stdlib.h>
#define max 21
struct node
{
char data;
struct node *l,*r;
};
char s[51];
int top;
struct node *creat()//结构体函数->返回结构体
{
struct node *root;
top++;
//top提前++,我之前放在return前面++报错,
//是因为return前面有无数个循环,都没有来得及把top++
if(s[top]==','){
return root=NULL;
}else {
root=(struct node *)malloc(sizeof(struct node));
root->data=s[top];
root->l=creat();
root->r=creat();
}
return root;
}
void zhongxu(struct node *root)
{
if(root)
{
zhongxu(root->l);
printf("%c",root->data);
zhongxu(root->r);
}
}
void houxu(struct node *root)
{
if(root)
{
houxu(root->l);
houxu(root->r);
printf("%c",root->data);
}
}
int main()
{
while(~scanf("%s",s))
{
top=-1;//top给-1,因为循环一开始就要++
struct node *root;
root=creat();
zhongxu(root);
printf("\n");
houxu(root);
printf("\n");
}
return 0;
}
三:统计叶子数
Description
已知二叉树的一个按先序遍历输入的字符序列,如abc,,de,g,,f,,, (其中,表示空结点)。请建立二叉树并求二叉树的叶子结点个数。
Input
连续输入多组数据,每组数据输入一个长度小于50个字符的字符串。
Output
输出二叉树的叶子结点个数。
Sample
Input
abc,,de,g,,f,,,
Output
3
Hint
参考代码
#include <bits/stdc++.h>
using namespace std;
struct node {
char data;
struct node *l,*r;
};
char s[55];
int top;
int len;
int sum;
struct node *buildtree(){
struct node *tree;
top++;
if(top<len){
if(s[top]==','){
return tree=NULL;
}else {
tree=(struct node *)malloc(sizeof(struct node ));
tree->data=s[top];
tree->l=buildtree();
tree->r=buildtree();
}
}
return tree;
};
//输出二叉树看一下是否正确
void test(struct node *tree){
if(tree){
cout<<tree->data;
test(tree->l);
test(tree->r);
}
}
//计算叶子数
int sumleaves(struct node *tree){
if(tree){
if(tree->l==NULL&&tree->r==NULL){
sum++;
}
sumleaves(tree->l);
sumleaves(tree->r);
}
return sum;
}
int main()
{
while(~scanf("%s",s)){
struct node *tree;
top=-1;
len=strlen(s);
tree=buildtree();
//cout<<len<<endl;
//test(tree);
sum=0;
sumleaves(tree);
cout<<sum<<endl;
}
return 0;
}
四:(先序中序)还原二叉树
Description
给定一棵二叉树的先序遍历序列和中序遍历序列,要求计算该二叉树的高度。
Input
输入数据有多组,每组数据第一行输入1个正整数N(1 <= N <= 50)为树中结点总数,随后2行先后给出先序和中序遍历序列,均是长度为N的不包含重复英文字母(区分大小写)的字符串。
Output
输出一个整数,即该二叉树的高度。
Sample
Input
9
ABDFGHIEC
FDHGIBEAC
Output
5
参考代码
#include <bits/stdc++.h>
using namespace std;
struct node {
char data;
struct node *l,*r;
};
char s1[55],s2[55];
int len;
int hight;
struct node *buildtree(char s1[],char s2[],int len){
struct node *tree;
if(len<=0){
return NULL;
}
tree = (struct node *)malloc(sizeof(struct node));
tree->data=s1[0];//前序遍历的第一个就是根节点
char *p=s2;
for(int i=0;i<len;i++,p++){
if(*p==s1[0]){
break;
}
}
int lon=p-s2;//接下来要判断的左边长度
tree->l = buildtree(s1+1,s2,lon);//向左找
tree->r = buildtree(s1+1+lon,p+1,len-lon-1);//向右找
return tree;
};
//输出二叉树看一下是否正确
void test(struct node *tree){
if(tree){
cout<<tree->data;
test(tree->l);
test(tree->r);
}
}
//高度
int treehight(struct node *tree){
int hl,hr,max=0;
if(tree){//如果不为空,hight++
hl=treehight(tree->l);
hr=treehight(tree->r);
if(hl>hr){
max=hl;
}else{
max=hr;
}
return max+1;
}else{
return 0;
}
return max;
}
int main()
{
int n;
while(cin>>n){
cin>>s1>>s2;
struct node *tree;
top=-1;
len=strlen(s1);
tree=buildtree(s1,s2,len);
//cout<<len<<endl;
//test(tree);
hight=0;
hight=treehight(tree);
cout<<hight<<endl;
}
return 0;
}
五:层序遍历
Description
已知一个按先序输入的字符序列,如abd,,eg,,,cf,,,(其中,表示空结点)。请建立二叉树并求二叉树的层次遍历序列。
Input
输入数据有多行,第一行是一个整数t (t<1000),代表有t行测试数据。每行是一个长度小于50个字符的字符串。
Output
输出二叉树的层次遍历序列。
Sample
Input
2
abd,,eg,,,cf,,,
xnl,,i,,u,,
Output
abcdefg
xnuli
Hint
参考代码
#include <bits/stdc++.h>
using namespace std;
struct node {
char data;
struct node *l,*r;
};
char s[55];
int top;
int len;
struct node *buildtree(){
top++;
struct node *root;
if(top<len){
if(s[top]==','){
return root=NULL;
}else {
root=(struct node *)malloc(sizeof(struct node));
root->data=s[top];
root->l=buildtree();
root->r=buildtree();
}
}
return root;
};
//层序输出,记录每一个根节点,然后把根节点左右子树再次记录
void ceng(struct node *root){
int in=0;
int out=0;
struct node *q[110];
q[in++]=root;
while(in>out){
if(q[out]!=NULL){
cout<<q[out]->data;
q[in++]=q[out]->l;
q[in++]=q[out]->r;
}
out++;
}
}
//测试
void test(struct node *root){
if(root->l&&root->r){
cout<<root->data;
test(root->l);
test(root->r);
}
}
int main()
{
int t;
cin>>t;
while(t--){
struct node *root;
cin>>s;
len=strlen(s);
top=-1;
root=buildtree();
//test(root);
ceng(root);
cout<<endl;
}
return 0;
}
六:哈夫曼编码
Description
字符的编码方式有多种,除了大家熟悉的ASCII编码,哈夫曼编码(Huffman Coding)也是一种编码方式,它是可变字长编码。该方法完全依据字符出现概率来构造出平均长度最短的编码,称之为最优编码。哈夫曼编码常被用于数据文件压缩中,其压缩率通常在20%~90%之间。你的任务是对从键盘输入的一个字符串求出它的ASCII编码长度和哈夫曼编码长度的比值。
Input
输入数据有多组,每组数据一行,表示要编码的字符串。
Output
对应字符的ASCII编码长度la,huffman编码长度lh和la/lh的值(保留一位小数),数据之间以空格间隔。
Sample
Input
AAAAABCD
THE_CAT_IN_THE_HAT
Output
64 13 4.9
144 51 2.8
Hint
哈夫曼树
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
也就是说:权值最小的离根节点最远。
思路:按权值从小到大排序,小的先组合叶子节点,依次向上形成哈夫曼树。
参考答案
#include <bits/stdc++.h>
using namespace std;
int main()
{
char s[1100];
int t[1100];
int q[1100];
int len,la,top,rear,sum,x1,x2;
while(cin>>s){
len=strlen(s);
la=len*8;
//sort(s,s+len,greater<char>());
//cout<<s<<endl;
memset(t,0,sizeof(t));
for(int i=0;i<len;i++){
t[s[i]]++;
}
top=0;
for(int i=0;i<500;i++){
if(t[i]){
q[top++]=t[i];
}
}
//cout<<top<<endl;
sort(q,q+top);//从小到大排序
rear=0;
sum=0;
while(rear!=top){
x1=q[rear++];
if(rear!=top){
x2=q[rear++];
sum+=x1+x2;
q[top++]=x1+x2;
sort(q+rear,q+top);//从rear之后从小到大排序
}
}
printf("%d %d %.1f\n",la,sum,1.0*la/sum);
}
return 0;
}
七:叶子问题
Description
已知一个按先序输入的字符序列,如abd,,eg,,,cf,,,(其中,表示空结点)。请建立该二叉树并按从上到下从左到右的顺序输出该二叉树的所有叶子结点。
Input
输入数据有多行,每一行是一个长度小于50个字符的字符串。
Output
按从上到下从左到右的顺序输出二叉树的叶子结点。
Sample
Input
abd,,eg,,,cf,,,
xnl,,i,,u,,
Output
dfg
uli
Hint
参考代码
#include <bits/stdc++.h>
using namespace std;
struct node {
char data;
struct node *l,*r;
};
int top,len;
char s[1010];
struct node *buildtree(){
struct node *root;
top++;
if(top<len){
if(s[top]==','){
return root=NULL;
}else {
root=(struct node *)malloc(sizeof(struct node ));
root->data=s[top];
root->l=buildtree();
root->r=buildtree();
}
}
return root;
};
//层序遍历输出叶子节点
void leaves(struct node *root){
int i=0,j=0;
struct node *b[110];
b[j++]=root;
while(i<j){
if(b[i]){
int flag=0;
b[j++]=b[i]->l;
if(b[i]->l==NULL)flag++;
b[j++]=b[i]->r;
if(b[i]->r==NULL)flag++;
if(flag==2)cout<<b[i]->data;
}
i++;
}
}
int main()
{
while(cin>>s){
struct node *root;
len=strlen(s);
top=-1;
root=buildtree();
leaves(root);
cout<<endl;
}
return 0;
}
八:(中序后序)求二叉树的深度
Description
已知一颗二叉树的中序遍历序列和后序遍历序列,求二叉树的深度。
Input
输入数据有多组,输入T,代表有T组数据。每组数据包括两个长度小于50的字符串,第一个字符串表示二叉树的中序遍历,第二个表示二叉树的后序遍历。
Output
输出二叉树的深度。
Sample
Input
2
dbgeafc
dgebfca
lnixu
linux
Output
4
3
参考代码
#include <bits/stdc++.h>
using namespace std;
struct node {
char data;
struct node *l,*r;
};
char s1[55],s2[55];
int len;
int hight;
struct node *buildtree(char s1[],char s2[],int len){
struct node *tree;
if(len<=0){
return NULL;
}
tree = (struct node *)malloc(sizeof(struct node));
tree->data=s2[len-1];//后序遍历的最后一个就是根节点
char *p=s1;
for(int i=0;i<len;i++,p++){//在中序中找到根节点
if(*p==s2[len-1]){
break;
}
}
int lon=p-s1;//接下来要判断的左边长度(中序的根左边的长度)
tree->l = buildtree(s1,s2,lon);//向左找
tree->r = buildtree(s1+1+lon,p+1,len-lon-1);//向右找
return tree;
};
//正序输出二叉树看一下是否正确
void test(struct node *tree){
if(tree){
cout<<tree->data;
test(tree->l);
test(tree->r);
}
}
//高度
int treehight(struct node *tree){
int hl,hr,max=0;
if(tree){//如果不为空,hight++
hl=treehight(tree->l);
hr=treehight(tree->r);
if(hl>hr){
max=hl;
}else{
max=hr;
}
return max+1;
}else{
return 0;
}
return max;
}
int main()
{
int t;
cin>>t;
while(t--){
cin>>s1>>s2;
struct node *tree;
len=strlen(s1);
tree=buildtree(s1,s2,len);
//cout<<len<<endl;
//test(tree);
hight=0;
hight=treehight(tree);
cout<<hight<<endl;
}
return 0;
}




评论区