遥感图像场景识别
源代码及数据集:
链接:https://pan.baidu.com/s/1an5usnvJFjQZjkClpWwxDA
提取码:gglf
Ⅰ、项目任务要求
*任务描述:*
遥感图像为我们提供了丰富的地球地貌信息,包括:城市、森林、农业、草原、港口、公路、海洋等,通过对遥感图像进行判读和分类,可以准确地获取森林覆盖率、农田覆盖率、城市发展概况、交通建设进度等信息。因此,对遥感图像进行处理、分析、判别具有重要的社会价值。
遥感图像场景分类是遥感领域近年来的热门研究课题。其主要过程是根据提取的图像特征从多幅图像中区分出具有相似场景特征的图像,并对这些图像赋予正确的类别标签。因此,如何准确学习遥感图像特征并从中获取有价值的场景语义信息,是遥感图像场景分类的关键。
传统遥感图像场景分类方法的关键在于人工提取图像特征,然而由于遥感技术的迅速发展,图像的分辨率在与日俱增,高分辨率图像比低分辨率图像包含的信息和细节特征更加丰富,再加上遥感图像本身的复杂背景和尺度多样化,导致传统分类方法已无法高效地提取到更具代表性的图像特征,这正是遥感图像场景分类面临的一个难点。
近年来,深度学习在机器学习领域发展迅猛,并在自然语言处理、语音识别和图像识别等方面取得了许多令人瞩目的成果。深度学习方法通过训练大量的样本数据可以挖掘到其中的内在规律和表达层次,从而形成高级的特征表达。这一优势有效地解决了传统分类方法的问题,因此深度学习方法也广泛应用于遥感图像处理领域。卷积神经网络是目前一种应用非常广泛的深度学习模型架构,近年来占据着遥感图像场景识别研究的主导地位。
此实验内容:****分别用PCA+SVM、softmax、CNN三种分类方法对********UCMerced_LandUse********公共数据集进行分类,并写出实验结果分析。****
主要任务要求(必须完成以下内容但不限于这些内容):
1、UCMerced_LandUse数据集采用公共数据集。
2、简述三种算法思想和实现原理。
3、写出实验结果分析:
(1) 数据集描述。包括数据集介绍、训练集和测试集介绍等。
(2) 实验运行环境描述。如开发平台、编程语言、调参情况等。
(3) 三种方法对****UCMerced_LandUse****数据集分类识别结果分析(****三种方法识别对比率表及结果分析****)。
*三种方法对********UCMerced_LandUse********数据集的识别效果对比*
| 方法结果对比 | PCA+SVM | softmax | CNN |
|---|---|---|---|
| 识别率(%) | 24.9% | 21.3% | 33.0% |
II、方法思想及实现原理陈述(20分)
*1.PCA+SVM:*
主成分分析 ( Principal Component Analysis , PCA )或者主元分析。是一种掌握事物主要矛盾的统计分析方法,它可以从多元事物中解析出主要影响因素,揭示事物的本质,简化复杂的问题。计算主成分的目的是将高维数据投影到较低维空间。
首先将数据库里面整理好的数据导出为一个矩阵,然后按照同意和拒绝分为两类加上标签,用0代表拒绝,1代表同意(这一步会在后面的模型训练中用到)。
然后先降维,利用princomp函数将导出的矩阵作为输入,由于数据每个属性大小差别颇大,我们会利用协方差进行相应的处理,这一步不会对后面的结果有影响,只是对数值进行处理,便于后面的降维操作。princomp函数会输出4个参数其中latent是协方差矩阵的特征值,coef是输入矩阵所对应的协方差矩阵的所有特征向量组成的矩阵,即变换矩阵,我们利用latent取出coef前约90%的主成分与输入矩阵相乘所得到的的新的矩阵就是我们想要矩阵,这个过程也将原来的维数降低,同时将原有的坐标转换到新的坐标下。
再训练模型,首先我们将上面得到的新的数据和开始的时候提到的标签,利用交叉检验的原理,平均分成五分,将其中四份用作训练,一份作为测试交叉检验。训练主要利用svmtrain函数将上面得到四份数据作为输入,可以得到一个模型model。这个就是我们所要训练的模型。
最后利用svmpredict函数将测试数据和相应的标签作为输出,得出最后的准确率。
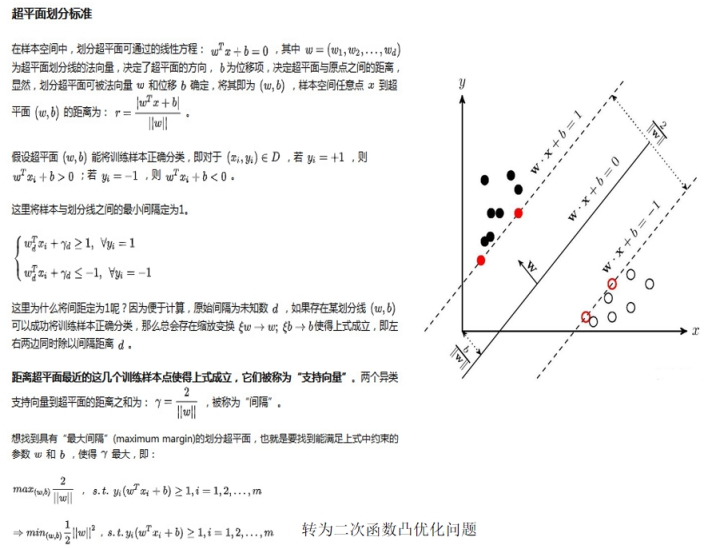
优点:
有效处理非线性分类问题;不需要预先确定分类函数的基本结构;
该方法有扎实的理论保证(统计学习理论)﹔
不容易出现过拟合;
优化算法是凸二次规划问题,有高效的实现。
*2.********Softmax********:*
softmax逻辑回归模型是logistic回归模型在多分类问题上的推广,在多分类问题中,类标签y可以取两个以上的值。 Softmax回归模型对于诸如MNIST手写数字分类等问题是很有用的。
softmax用于多分类过程中,它将多个神经元的输出,映射到(0,1)区间内,可以看成概率来理解,从而来进行多分类!

*3.********CNN********:*
卷积神经网络(CNN)最擅长的就是图片的处理。它受到人类视觉神经系统的启发。
与常规神经网络不同,卷积神经网络的各层中的神经元是3维排列的:宽度、高度和深度。其中的宽度和高度是很好理解的,因为本身卷积就是一个二维模板,但是在卷积神经网络中的深度指的是激活数据体的第三个维度,而不是整个网络的深度,整个网络的深度指的是网络的层数。举个例子来理解什么是宽度,高度和深度,假如使用CIFAR-10中的图像是作为卷积神经网络的输入,该输入数据体的维度是32x32x3(宽度,高度和深度)。我们将看到,层中的神经元将只与前一层中的一小块区域连接,而不是采取全连接方式。对于用来分类CIFAR-10中的图像的卷积网络,其最后的输出层的维度是1x1x10,因为在卷积神经网络结构的最后部分将会把全尺寸的图像压缩为包含分类评分的一个向量,向量是在深度方向排列的。
卷积神经网络主要由这几类层构成:输入层、卷积层,ReLU层、池化(Pooling)层和全连接层(全连接层和常规神经网络中的一样)。通过将这些层叠加起来,就可以构建一个完整的卷积神经网络。在实际应用中往往将卷积层与ReLU层共同称之为卷积层,所以卷积层经过卷积操作也是要经过激活函数的。具体说来,卷积层和全连接层(CONV/FC)对输入执行变换操作的时候,不仅会用到激活函数,还会用到很多参数,即神经元的权值w和偏差b;而ReLU层和池化层则是进行一个固定不变的函数操作。卷积层和全连接层中的参数会随着梯度下降被训练,这样卷积神经网络计算出的分类评分就能和训练集中的每个图像的标签吻合了。
III、实验结果分析(30分)
(1) 数据集描述。包括数据集介绍、训练集和测试集介绍等。
共包含21类类型图片,每类100张,每张像素大小为256*256,数据类内距离大,类间小。
训练集测试集7:3的比例,前70%为训练集,后30%为测试集。
(2) 实验运行环境描述。如开发平台、编程语言、调参情况等。
运行环境为python的sklearn平台和pytorch平台
(3) 三种方法对UCMerced_LandUse数据集分类识别结果分析(三种方法识别对比率表及结果分析)。
三种方法对UCMerced_LandUse数据集的识别效果对比
*三种方法对********UCMerced_LandUse********数据集的识别效果对比*
| 方法结果对比 | PCA+SVM | softmax | CNN |
|---|---|---|---|
| 识别率(%) | 24.9% | 21.3% | 33.0% |
PCA+SVM实验结果:

Softmax实验结果:
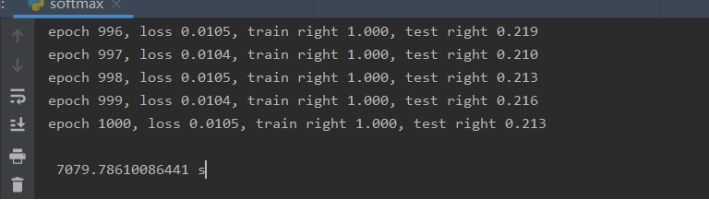
cnn实验结果:
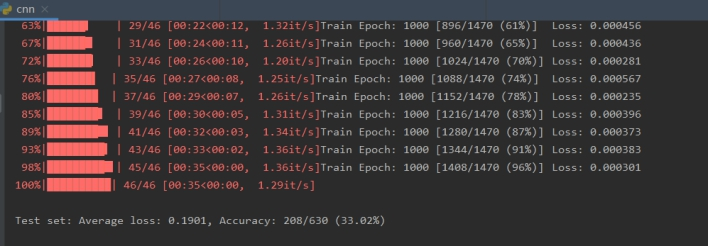
由实验结果可知PCA+SVM准确率为24.9%,softmax(1000次)准确率为21.3%,cnn(1000次)准确率为33.0%,对比准确率分析为:cnn在此实验中的分类效果更好。
IV、代码实现(50分)
PCA+SVM
#导入模块
import cv2 # openCV模块用于图像处理
import numpy as np
from sklearn.model_selection import train_test_split # 用于切分训练集和测试集
from sklearn.decomposition import PCA # PCA降维
from sklearn.svm import SVC # 支持向量机
data=[] # 存放图像数据
label=[] # 存放标签
for i in range(1, 22):
for j in range(1, 101):
path='UCMerced_LandUse2/'+'s'+str(i)+'/'+str(j)+'.tif'
img=cv2.imread(path, cv2.IMREAD_GRAYSCALE)
h,w=img.shape
img_col = img.reshape(h*w)
data.append(img_col)
label.append(i)
C_data = np.array(data)
C_label = np.array(label)
# 切分数据集
x_train, x_test, y_train, y_test = train_test_split(C_data, C_label, test_size=0.3, random_state=224)
pca = PCA(n_components=0.9, svd_solver='auto').fit(x_train)
# 降维
x_train_pca = pca.transform(x_train)
x_test_pca = pca.transform(x_test)
svc = SVC(kernel='linear')
svc.fit(x_train_pca, y_train)
# 测试识别准确度
print('%.5f'%svc.score(x_test_pca, y_test))
CNN
import torch
import torch.nn.functional as F
import torch.nn as nn
from torch.utils.data import dataset
from torchvision import transforms
from torch.autograd import Variable
from tqdm import tqdm
from torchvision.datasets import ImageFolder
import torch.optim as optim
# Training settings
batch_size = 32
####
data_transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(mean=[0.5, 0.5, 0.5], std=[0.5, 0.5, 0.5])
])
train_dataset = ImageFolder(r".\dataset\train", transform=transforms.Compose([
transforms.Resize((224, 224)),
transforms.ToTensor()
]))
train_loader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
test_dataset = ImageFolder(r".\dataset\val_dirs", transform=transforms.Compose([
transforms.Resize((224, 224)),
transforms.ToTensor()
]))
test_loader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=False)
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Sequential(
nn.Conv2d( # (3,224,224)
in_channels=3,
out_channels=16,
kernel_size=5,
stride=1,
padding=2 # padding=(kernelsize-stride)/2
), # (16,224,224)
nn.ReLU(),
nn.MaxPool2d(kernel_size=2) # (16,112,112)
)
self.conv2 = nn.Sequential( # (16,112,112)
nn.Conv2d(16, 32, 5, 1, 2), # (32,112,112)
nn.ReLU(), # (32,112,112)
nn.MaxPool2d(2) # (32,56,56)
)
self.out = nn.Linear(32*56*56, 21)
# 定义前向传播过程,过程名字不可更改,因为这是重写父类的方法
def forward(self, x):
x = self.conv1(x)
x = self.conv2(x) # (batch,32,56,56)
x = x.view(x.size(0), -1) # (batch,32*56*56)
output = self.out(x)
return F.log_softmax(output, dim=1)
model = Net()
optimizer = optim.SGD(model.parameters(), lr=0.0001, momentum=0.9)
def train(epoch):
# 每次输入barch_idx个数据
for batch_idx, (data, target) in enumerate(tqdm(train_loader)):
data, target = Variable(data), Variable(target)
optimizer.zero_grad()
output = model(data)
# loss
loss = F.nll_loss(output, target)
loss.backward()
# update
optimizer.step()
if batch_idx % 2 == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f} '.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
def test():
test_loss = 0
correct = 0
# 测试集
for data, target in test_loader:
# data, target = Variable(data, volatile=True), Variable(target)
output = model(data)
# sum up batch loss
test_loss += F.nll_loss(output, target).item()
# get the index of the max
pred = output.data.max(1, keepdim=True)[1]
correct += pred.eq(target.data.view_as(pred)).cpu().sum()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\t'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
for epoch in range(1,1001):
train(epoch)
test()
softmax
import torch
from torch.utils.data import dataset
from torchvision import datasets, transforms
from time import time
import numpy as np
from torchvision.datasets import ImageFolder
# Training settings
batch_size = 16
num_outputs = 21
num_epochs,lr = 1000,0.001
####
data_transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(mean=[0.5, 0.5, 0.5], std=[0.5, 0.5, 0.5])
])
train_dataset = ImageFolder(r".\dataset\train", transform=transforms.Compose([
transforms.Resize((224, 224)),
transforms.ToTensor()
]))
train_loader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
test_dataset = ImageFolder(r".\dataset\val_dirs", transform=transforms.Compose([
transforms.Resize((224, 224)),
transforms.ToTensor()
]))
test_loader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=False)
# 初始化参数与线性回归也类似,权重参数设置为均值为0 标准差为0.01的正态分布;偏差设置为0
W = torch.tensor(np.random.normal(0, 0.01, (3*224*224, num_outputs)), dtype=torch.float)
b = torch.zeros(num_outputs, dtype=torch.float32)
# 同样的,开启模型参数梯度
W.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)
def softmax(X):
X_exp = X.exp()
partition = X_exp.sum(dim=1, keepdim=True)
return X_exp / partition # 这部分用了广播机制
def net(X):
return softmax(torch.mm(X.view((-1, 3*224*224)), W) + b)
def cross_entropy(y_hat, y):
return -torch.log(y_hat.gather(1, y.view(-1, 1)))
def accuracy(y_hat, y):
return (y_hat.argmax(dim=1).float().mean().item())
def net_accurary(data_iter, net):
right_sum, n = 0.0, 0
for X, y in data_iter:
# 从迭代器data_iter中获取X和y
right_sum += (net(X).argmax(dim=1) == y).float().sum().item()
# 计算准确判断的数量
n += y.shape[0]
# 通过shape[0]获取y的零维度(列)的元素数量
return right_sum / n
def sgd(params, lr, batch_size):
# lr:学习率,params:权重参数和偏差参数
for param in params:
param.data -= lr * param.grad / batch_size
def train_softmax(net, train_loader, test_loader, loss, num_epochs, batch_size, params, lr, optimizer, net_accuracy):
for epoch in range(num_epochs):
# 损失值、正确数量、总数 初始化。
train_l_sum, train_right_sum, n = 0.0, 0.0, 0
for X, y in train_loader:
y_hat = net(X)
l = loss(y_hat, y).sum()
# 数据集损失函数的值=每个样本的损失函数值的和。
if params is not None and params[0].grad is not None:
for param in params:
param.grad.data.zero_()
l.backward() # 对损失函数求梯度
optimizer(params, lr, batch_size)
train_l_sum += l.item()
train_right_sum += (y_hat.argmax(dim=1) == y).sum().item()
n += y.shape[0]
test_acc = net_accurary(test_loader, net) # 测试集的准确率
print('epoch %d, loss %.4f, train right %.3f, test right %.3f' % (epoch + 1, train_l_sum / n, train_right_sum / n, test_acc))
time1 = time()
train_softmax(net, train_loader, test_loader, cross_entropy, num_epochs, batch_size, [W, b], lr, sgd, net_accurary)
print('\n', time() - time1, 's')
#X, y = iter(test_loader).next()




评论区